搜索到
16
篇与
的结果
-
-
-
-
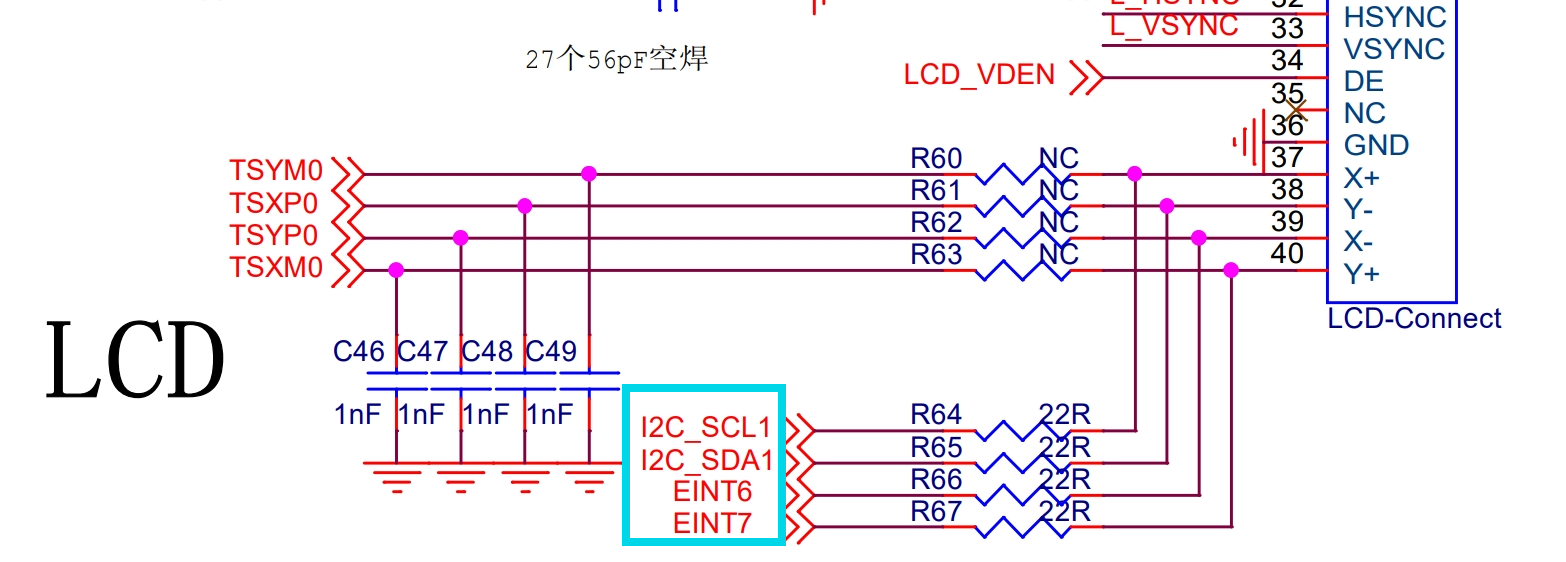
S5PV210 (Study210)裸机移植触摸屏驱动 前言最近在做嵌入式作业的裸机开发部分，看到板子在Linux下触摸屏是支持单点触控的，然而在裸机提供的示例程序中并没有提供触摸屏相关驱动，因此在Linux驱动的基础上进行了移植从而在裸机下同样支持触摸操作1.获取电容屏型号查阅数据手册及原理图通过查询S5PV210的数据手册，可以看到其包含了8个ADC引脚用于电阻屏的接入（可以接两块），然而对于Study210开发板来说，通过对Linux下的触摸进行测试，初步判断屏幕为电容屏，电容屏一般是通过I2C驱动，因此需要寻找板子上的I2C引脚。通过查看Study210的原理图可知，LCD显示接口上有I2C相关引脚，推测用于触摸。通过原理图可以看到，通过I2C1与电容屏进行通信，两个GPIO推测一个用于供电，一个用于产生触摸中断。然而I2C通信还需要知道设备的地址等信息，也就意味着需要知道电容屏的型号以及其数据手册，才能实现与电容屏的通信。查找Linux驱动程序源码因为Linux下可以正常驱动电容屏，因此可以在Linux下查看设备型号以及对应驱动程序。（LInux查看input，查看设备信息）据此，我们得到了电容屏的型号为gslx680。在Linux内核源码中，可以找到gslx680驱动的源码，但是由于其依赖于Linux库，因此不能简单移植到裸机上使用，不过从源码中可以得知，EINT7为中断引脚，EINT6为供电引脚。因此，I2C的实现以及触摸屏的驱动需要我们进行手动实现。查询电容屏数据手册GSLX680引脚定义通过搜索gslx680，我们可以找到其 介绍 ，设备制造商同样只提供了Linux下的驱动但是给出了触摸屏的驱动原理。The chip has four main pins to communicate with a CPU:SDA and SCL: these two pins conform an I2C bus, allowing to exchange data between the chip and the main CPU.IOCNTL: this pin, when active (logic 1) enables the chip, making it to answer to I2C commands and read the touch screen. When inactive (logic 0), the chip is in Low Power state.INT: when there is data available (a press) or in other cases (not sure, not have enough documentation), this pin gets active to signal this to the CPU.可以看到其一共有4个引脚，SDA与SCL用于I2C通信，IOCNTL用于使能，INT用于产生触摸中断。GSLX680内部寄存器读写在文档的I2C Communication部分，介绍了设备的I2C地址以及设备的寄存器地址所代表的含义。可以看到设备的I2C地址为0x40。当I2C发送数据时，首先需要发送从设备的地址，在这里也就是0x40，随后才是发送的数据，I2C一次可以发送8位（一字节）。在文档中介绍，如果需要对gslx680的寄存器进行写入（后续设备初始化要用到），需要按照以下的格式。START(W) 0x40 0x10 0x00 0x01 0xF5 0x41 0xFF STOP即开始I2C写入后，首先写入设备地址0x40，随后写入需要被写入的寄存器地址0x10，接下来的内容是要被写入的数据（变长），最后是I2C终止信号。上述指令下，会往0x10地址写入数据0x00，往0x11地址写入数据0x01，往0x12地址写入0xF5以此类推。这样就可以通过I2C完成对gslx680内部寄存器的写入。文档中介绍，如果要读取GSLX680的内部寄存器，需要先以写入模式写入需要读取的地址，随后即可一直读取内容。例如如果需要读取0x80地址的5个字节内容，首先需要发送START(W) 0x40 0x80 STOP表示需要从0x80地址开始读取，随后切换到读取模式，读取5次发出停止信号，即可读取到0x80-0x84寄存器中的内容。文档中介绍了每一个寄存器所代表的含义：0x00-0x7F: these registers are used to load portions of the firmware0x80: contains the number of touches in the screen. If zero, the user isn't touching the screen; if one, only one finger is on the screen; if two, there are two fingers; and so on.0x84-0x87: contains the coordinates for the first touch.0x88-0x8B: contains the coordinates for the second touch.0x8C-0xAB: contains the coordinates for the third, fourth, and so on (up to five in some devices, up to ten in other), touches, in the same format than the previous ones (four bytes for each touch).0xE0: STATUS register0xE4, 0xBC-0xBF: some kind of control registers. Needed for uploading the firmware and soft resetting the chip (there's not more data available about them).0xF0: PAGE register. Contains the memory page number currently mapped in the 0x00-0x7F registers.可以看到0x00-0x7F地址包含了触摸屏的固件程序，固件包含在Linux驱动的.h头文件中。0x80地址包含了屏幕上被触摸的点的个数，这块屏幕支持多点触控，测试为10点触控（然而一般也用不着bushi）0x84-0x87包含了第一个触摸点的坐标，其他触摸点以此类推地址增加。0xE0是状态寄存器，用于控制触摸屏是否工作0xF0是分页寄存器，用于控制固件区域0x00-0x7F的分页（类似MMU），向其写入固件时，需要往多个分页内写入数据。（所以虽然0x00到0x7F一共才128个Byte，头文件内包含的固件有2000多行）接下来文档介绍了触摸屏的触摸点坐标格式。从上述描述中我们可以看到第一个触摸点的数据坐标是由0x84-0x87四个字节存储的，其中前两个字节存储x坐标，后两个字节存储y坐标。x坐标的低12位表示x的坐标值；y坐标的低12位表示y的坐标值，高4位表示触摸的手指编号（多点触控需要用）触摸屏，启动！随后文档介绍了触摸屏的初始化流程Enable the chip (set IOCTNL to 1) Reset the chip (explained later) Upload the firmware (explained later) Startup chip (set STATUS register to 0) Reset the chip Disable the chip (set IOCTNL to 0) Wait 50 ms Enable the chip (set IOCTNL to 1) Wait 30 ms Disable the chip (set IOCTNL to 0) Wait 5 ms Enable the chip (set IOCTNL to 1) Wait 20 ms Reset the chip Startup chip (set STATUS register to 0)可以看到初始化流程还是比较复杂的，（关关开开x），首先当然要上电，设置IOCTNL为高电平，随后进行Resetset the STATUS register to 0x88 wait 10 ms set register 0xE4 to 0x04 wait 10 ms set registers 0xBC-0xBF to 0x00 wait 10 ms.Reset需要设置状态寄存器以及部分寄存器的内容，即利用我们上面介绍的I2C写入方式对这些寄存器进行操作。同时我们可以看到，其中有一步是Upload the firmware，触摸屏内部不含有固件，需要每次通过I2C进行写入。固件包含在gslx680.h中，上文我们介绍了固件在gslx680中是分页存储的，每一页的内容描述如下：{0xf0,0x3}, {0x00,0xa5a5ffc0}, {0x04,0x00000000}, {0x08,0xe810c4e1}, {0x0c,0xd3dd7f4d}, {0x10,0xd7c56634}, {0x14,0xe3505a2a}, {0x18,0x514d494f}, {0x1c,0x5836e48b}, {0x20,0x00000000}, {0x24,0x00000000}, {0x28,0x00000000}, {0x2c,0x00000000}, {0x30,0x00001000}, {0x34,0x00000000}, {0x38,0x00000000}, {0x3c,0x00000000}, {0x40,0x00000001}, {0x44,0x00000000}, {0x48,0x00000000}, {0x4c,0x00000000}, {0x50,0x00000000}, {0x54,0x01020304}, {0x58,0x05060708}, {0x5c,0x090a0b0c}, {0x60,0x0d0e0e0f}, {0x64,0x10111213}, {0x68,0x14151617}, {0x6c,0x18191a1b}, {0x70,0x1b1c1e1f}, {0x74,0x00000000}, {0x78,0x00010000}, {0x7c,0x8c846af3},即首先向0xf0写入0x3表示切换到0x3分页，随后向0x00写入4个Byte，以此类推直到0x7C。当然根据我们上面介绍了I2C的特点，你也可以直接向0x00地址写入128个Byte（事实上这样速度更快）这样的分页在头文件中一共有145个，可以使用循环进行写入。按照以上流程，进行初始化后，触摸屏就可以正常使用了，当有点击的时候，EINT7引脚会触发中断，此时读取0x80地址以及0x84-0x87地址即可获取触摸点坐标。
-
自动控制原理第三章笔记 第三章 时域分析法典型控制过程及性能指标典型控制信号单位阶跃信号$ L[1(t)] = \frac1s $单位斜坡信号$ L[t \times 1(t)] = \frac{1}{s^2} $单位脉冲信号$ L[\delta(t)] = 1 $正弦信号$ L[Asin\omega_0t] = \frac{A\omega_0}{s^2 + \omega^2} $单位抛物线信号$ L[\frac{Rt^2}{2} \times 1(t)] = \frac{R}{s^3} $性能指标（以阶跃响应为例）延迟时间 $ t_d $ ：响应上升到 $ y(\infty) $ 的 50% 时所需时间。上升时间 $ t_r $ ：响应上升到稳态值 $ y(t_r) $ 时所需时间。峰值时间 $ t_p $ ：响应超过稳态值到达第一个峰值（极大值）时所需时间。超调量 $ \sigma \% $ ：$ \frac{y(t_p)-y(\infty)}{y(\infty)} \times 100\%$。调节时间 $ t_s $ ：达到稳态过程的时间，即进入5%或者2%误差带所需时间。震荡次数 $ N $ ：到达稳态时间之前穿过稳态值次数的一半对于单调上升的单位阶跃响应来说，由于其没有震荡和超调量，因此一般用 $ t_s $ 表示调节的快速性， $ t_r $ 定义为由稳态值的10%上升至90%所用时间。一阶系统的时域分析数学模型一阶系统的闭环传递函数为：$$ \Phi(s) = \frac{Y(s)}{R(s)} = \frac{1}{Ts+1} $$其中 $ T $ 称为时间常数一阶系统单位阶跃响应输入 $ R(s) = \frac1s $输出 $ Y(s) = \frac{1}{s(Ts+1)} $取反变换得 $ y(t) = 1-e^{-t/T} $稳态值为1，呈单调上升， $ t=0 $ 时斜率为 $ 1/T $$ t_s=3T $ 对应5%误差带， $ t_s=4T $ 对应2%误差带因为最终数值 $ y(\infty) = 1 $ ，因此不存在稳态误差一阶系统单位斜坡响应输入 $ R(s) = \frac{1}{s^2} $输出 $ Y(s) = \frac{1}{s^2(Ts+1)} $反变换得 $ y(t) = t-T+T\cdot e^{-t/T} $稳态值为 $ t-T $ ，稳态误差为 $ T $稳态输出与输入的斜率相等，但是存在着 $ T $ 的滞后一阶系统单位脉冲响应输入 $ R(s) = 1 $输出 $ Y(s) = \frac{1}{Ts+1} $反变换得 $ y(t) = \frac1Te^{-t/T} $呈单调递减且最终趋于0改善一阶系统性能一阶系统的性能取决于时间常数 $ T $ 的影响，因此可以改变闭环传递函数从而对时间常数进行调整，有引入常值负反馈和前向通道串联放大两种方式常值负反馈即由单位负反馈变为常值 $ \alpha $ 的负反馈，对于 $ G(s)=\frac{1}{Ts+1} $ 调整后传递函数为$$ \Phi(s) = \frac{\frac{1}{Ts+1}}{1+\frac{\alpha}{Ts+1}} = \frac{\frac{1}{1+\alpha}}{\frac{T}{1+\alpha}s+1} $$可见 $ \alpha $ 越大，新的传递函数的时间常数越小前向通道串联放大对于单位负反馈系统的开环传递函数 $ G(s) =\frac{k}{s} $ 其时间常数为 $ \frac{1}{k} $ ，若在其之前加入一个放大环节，即新的开环传递函数为 $ \frac{\alpha k}{s} $ ，其时间常数为 $ \frac{1}{\alpha k} $二阶系统的时域分析二阶系统的数学模型$$ \Phi(s) = \frac{\theta_c(s)}{\theta_r(s)} = \frac{k}{Js^2+Fs+k} $$其特征方程为$$ Js^2+Fs+k=0 $$引入参量 $ \omega_n^2 = \frac{k}{J} $ ， $ 2\zeta\omega_n = \frac{F}{J} $其中 $ \omega_n $ 称为无阻尼自然频率或固有频率， $ \zeta $ 为无量纲的阻尼系数，又称为阻尼比（实际阻尼系数/临界阻尼系数）二阶系统的特征根分析由上述参量代换后，二阶系统的特征方程可以化为$$ s^2+2\zeta\omega_ns+\omega_n^2 = 0 $$特征方程的根为$$ s_{1,2} = -\zeta\omega_n \pm \omega_n\sqrt{\zeta^2-1} $$随着 $ \zeta $ 取值的不同，特征根的位置不同$ 0<\zeta<1 $ 时，系统有负实部的共轭复根，此时为欠阻尼状态$$ s_{1,2} = -\zeta\omega_n \pm j\omega_n\sqrt{1-\zeta^2} $$$ \zeta=1 $ 时，系统有一对相等的负实根，此时为临界阻尼状态$$ s_{1,2} = -\zeta\omega_n $$$ \zeta>1 $ 时，系统有两个不相等的负实根，此时为过阻尼状态$$ s_{1,2} = -\zeta\omega_n \pm j\omega_n\sqrt{1-\zeta^2} $$$ \zeta = 0 $ 时，系统有两个纯虚根，此时为无阻尼状态$$ s_{1,2} = \pm j\omega_n\sqrt{1-\zeta^2} $$二阶系统的单位阶跃响应二阶系统的单位阶跃响应取决于其阻尼系数的大小，当阻尼系数 $ \zeta\geq1 $ 时，响应为无超调的单调上升曲线，当阻尼系数 $ 0<\zeta<1 $ 时，系统会发生震荡， $ \omega_d = \omega_n\sqrt{1-\zeta^2} $ 称为震荡角频率，当 $ \zeta=0 $ 时处于无阻尼状态，系统进行等幅振荡，角频率为 $ \omega_n $ 在欠阻尼系统中，对于一定的阻尼比 $ \zeta $ ， $ \omega_n $ 越大，则调节时间 $ t_s $ 越小，速度越快，但系统响应的平稳性会越差最佳阻尼比 $ \zeta=0.707(\frac{\sqrt{2}}{2}) $欠阻尼二阶系统单位阶跃响应的性能指标上升时间 $ t_r $$ t_r = \frac{\pi-\theta}{\omega_d} $其中 $ \theta $ 为弧度峰值时间 $ t_p $$ t_p = \frac{\pi}{\omega_d} $超调量 $ \sigma $$ \sigma\% = e^{\frac{-\zeta\pi}{\sqrt{1-\zeta^2}}} \times 100\% $调节时间 $ t_s $$ t_s = \frac{4}{\zeta\omega_n} (\Delta = 2\%)$$ t_s = \frac{3}{\zeta\omega_n} (\Delta = 5\%)$震荡次数 $ N $$ N = \frac{t_s}{\omega_d} $
